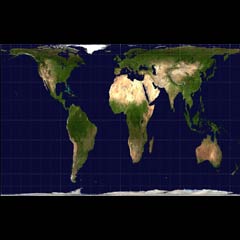
 Plasmar una superficie curva, como la Tierra, en otra plana, como un mapa, requiere inevitablemente de una deformación de ángulos o de superficie. A diferencia del mapamundi empleado comúnmente, el mapa de Peters se basa en la conservación de los ángulos y sitúa el ecuador en el centro del mapa, dando así la misma importancia a los países del hemisferio norte que a los países del hemisferio sur.
Plasmar una superficie curva, como la Tierra, en otra plana, como un mapa, requiere inevitablemente de una deformación de ángulos o de superficie. A diferencia del mapamundi empleado comúnmente, el mapa de Peters se basa en la conservación de los ángulos y sitúa el ecuador en el centro del mapa, dando así la misma importancia a los países del hemisferio norte que a los países del hemisferio sur.
El resultado es que el número de km2 de los continentes es más equilibrado con respecto al tamaño que los continentes poseen en el mapa. De este modo, África es más grande y Europa es más pequeña de lo que son en el mapamundi más utilizado.
La ONU y las ONG defienden la validez del mapa de Peters por dar una imagen más ajustada del mundo, sin embargo, su aplicación no se ha extendido, según las ONG, porque la proyección de Peters resta importancia a los países más poderosos con respecto a los países del 3º mundo.
La proyección de Peters también se conoce como proyección de Gall-Peters, ya que el clérigo escocés James Gall ya propuso en 1855 el mismo sistema aplicado por Peters más tarde, a mediados del siglo XX.
La Proyección de Peters (llamada así por Arno Peters), aunque lo correcto sería Proyección de Gall-Peters es una proyección cartográfica que apareció por primera vez en 1856, publicada en el Polish Geographical Magazine por James Gall.
Índice [ocultar]
1 Obtención
1.1 Discusión
2 Descripción
3 Véase también
4 Referencias
5 Enlaces externos
Obtención[editar]
Fórmula:
begin{align}
x &= Rlambda\
y &= 2Rsinvarphi
end{align}
Donde λ es la longitud desde el meridiano central (en radianes), φ es la latitud y R es el radio de la esfera tomada de modelo, del globo terráqueo1 . Por lo tanto la esfera se proyecta sobre un cilindro vertical, y el cilindro se estira al doble de su longitud. El factor de estiramiento, 2 en este caso.
Con esta proyección que mantiene la superficie real de los países, pero formas y distancias son modificadas. Existe una versión modificada de este mapa, donde las formas son menos deformadas2 .
Discusión[editar]
Las diversas especializaciones de la proyección de áreas cilíndrico difieren solamente en el radio del eje vertical al horizontal. Esta proporción determina el estándar paralelo de la proyección, la cual es paralela a la cual no hay distorsión en donde las distancias coinciden con la escala especificada. Siempre existen dos estándares paralelos en en la proyección del área equitativa, cada una con la misma distancia norte y sur al ecuador. Los paralelos estándar de la Gall-Peters son 45 ° N y 45 ° S. Varias otras especialidades de la igualdad de área cilíndrica se han descrito, promovido, o llamado de otro modo.
Descripción[editar]
La proyeccion de Petters es equiárea, representando proporcionalmente las áreas de las distintas zonas de la tierra.
En primer lugar, la «proyección de Peters» no existe; en todo caso existe el mapa de Peters o, más correctamente, el mapa de Gall-Peters. Una proyección es un conjunto de fórmulas (ecuaciones matemáticas) y Peters jamás se tomó la molestia de presentar ninguna ecuación, simplemente presentó un mapa ya dibujado (uno de los motivos es que una ecuación no se puede patentar, pero un mapa sí, y Peters lo registró y se hizo rico con los royalties). Aparte de eso, el mapa «de Peters» es sospechosamente parecido al mapa que hizo James Gall en el siglo XIX. Además es falso que el mapa de Gall-Peters conserve los ángulos como erróneamente se dice en el texto. El que sí que conserva los ángulos (y por eso es un mapa útil para la navegación) es la proyección de Mercator (el precio a pagar es que deforma las tierras más alejadas del Ecuador). El mapa de Gall-Peters conserva los tamaños relativos de los continentes (solo hasta cierto punto) a costa de deformar las áreas de los países (curiosamente, en el mapa de Gall-Peters los países más deformados son los del mal llamado Tercer Mundo, mientras que los del mal llamado Primer Mundo sufren una deformación menor, ¿no era éste un mapa solidario?) y a costa también de que en el mapa de Gall-Peters las distancias sean básicamente ficticias (por eso el mapa de Gall-Peters tampoco sirve para enseñar Geografía, a menos que por Geografía se entienda únicamente el tamaño relativo de los continentes).
Cuando Peters lanzó su delirante alegato anti-Mercator en los años 70, ya los cartógrafos señalaron los errores (y mala fe) de Peters. Hubo mucha gente que en un primer momento creyó, de buena fe, a Peters, pero que hoy, décadas después, se siga dando crédito y publicidad a las barbaridades de Peters es como para decir apaga y vámonos…
Mapamundis adecuados para enseñar Geografía los hay a patadas: el de Robinson, Winkel-Tripel, Goode, Mollweide… pero no ese estafador de Peters, por Dios.
Decirme como se elaboro el mapa de peters gracias
muy bueno pero yo hubiera puesto otra imagen.
Buenos días, Andoni:
En nuestro post nos hacemos eco de lo que podríamos decir es la «definición oficial» del mapa de Peters.
Como todo, el citado mapa es susceptible de crítica, así que agradecemos tu versión sobre el mismo. Se abre el debate…
Saludos.
En el texto hay una frase equivocada. En realidad la proyeción de Peters resta importancia a los países del tercer mundo (porque les desprecia y les deforma terriblemente)respecto a los del primer mundo, que les respeta como son.
Esto es evidente si miramos un globo terráqueo y lo comparamos con el mapa.
Además hay una manera muy sencilla de hacer áreas proporcionales sin deformar el tercer mundo. Pero entonces hay que deformar el primero ¿Dónde vendería Peters su mapa?
Peters desprecia al tercer mundo para conseguir fama y dinero.
la proyección de Peters resta importancia a los países de primer mundo porque al ser una proyección mas realista de lo que sería la superficie, países como USA y toda Europa son mucho mas pequeños que lo que se muestra en el mapa mundi que utilizamos comunmente